Sieving in parallel

It is likely that the first formal algorithm you ever learned was the Eratosthenes sieve. It is both easy and convenient for teaching children how to find the prime numbers under an upper bound.

You just need to prepare a table with all numbers between 2 and N and, methodically, look at the first uncrossed number, declare it the next found prime and cross out all its multiples until you run out of numbers. Take a look at this implementation or just delight yourself with this wonderful visualization by Peter Grill.

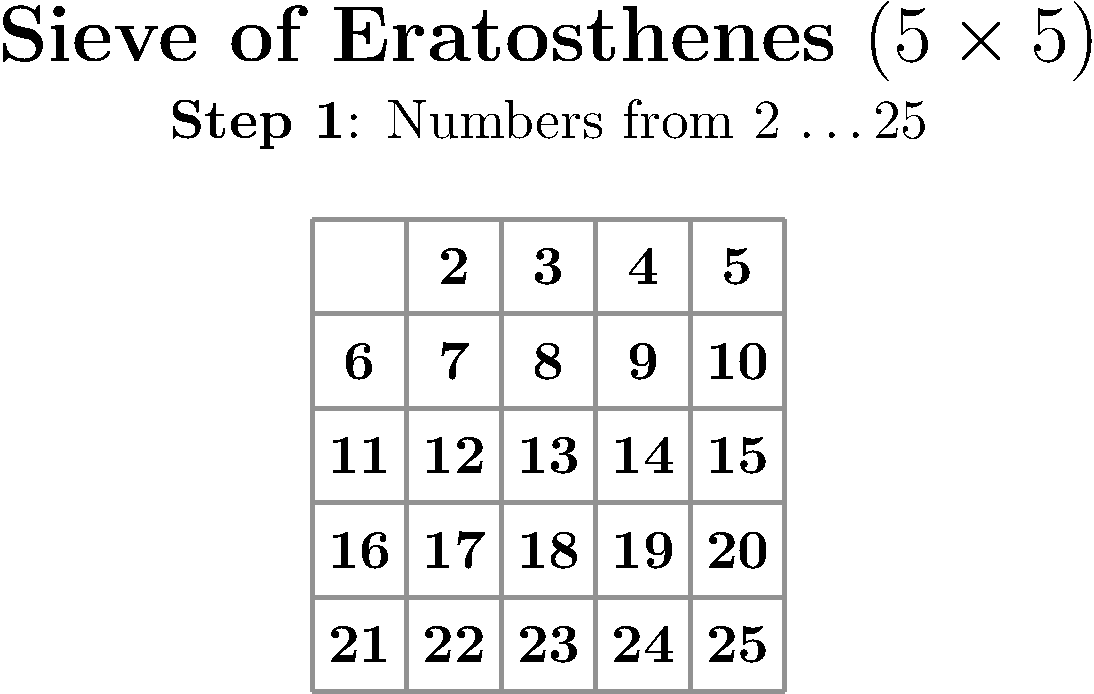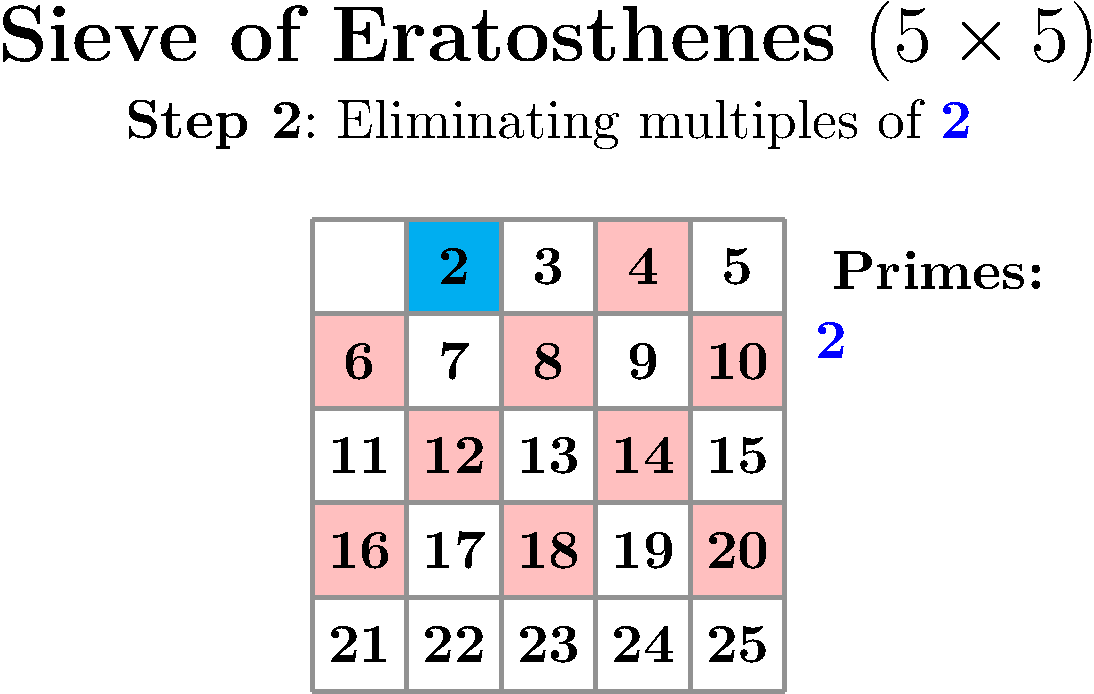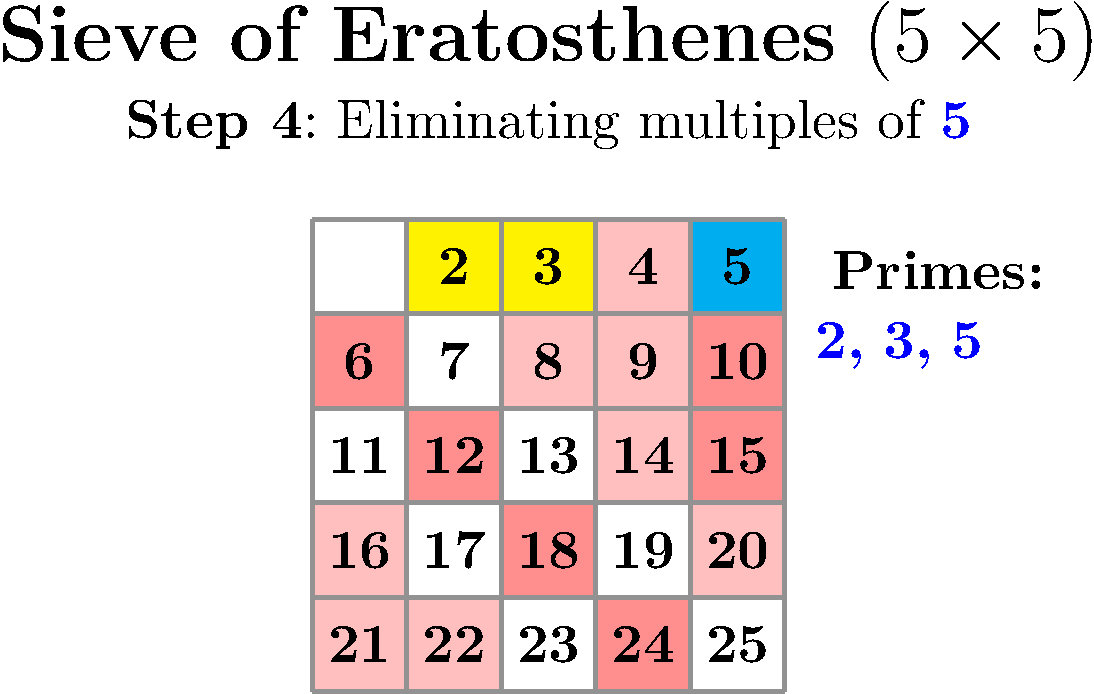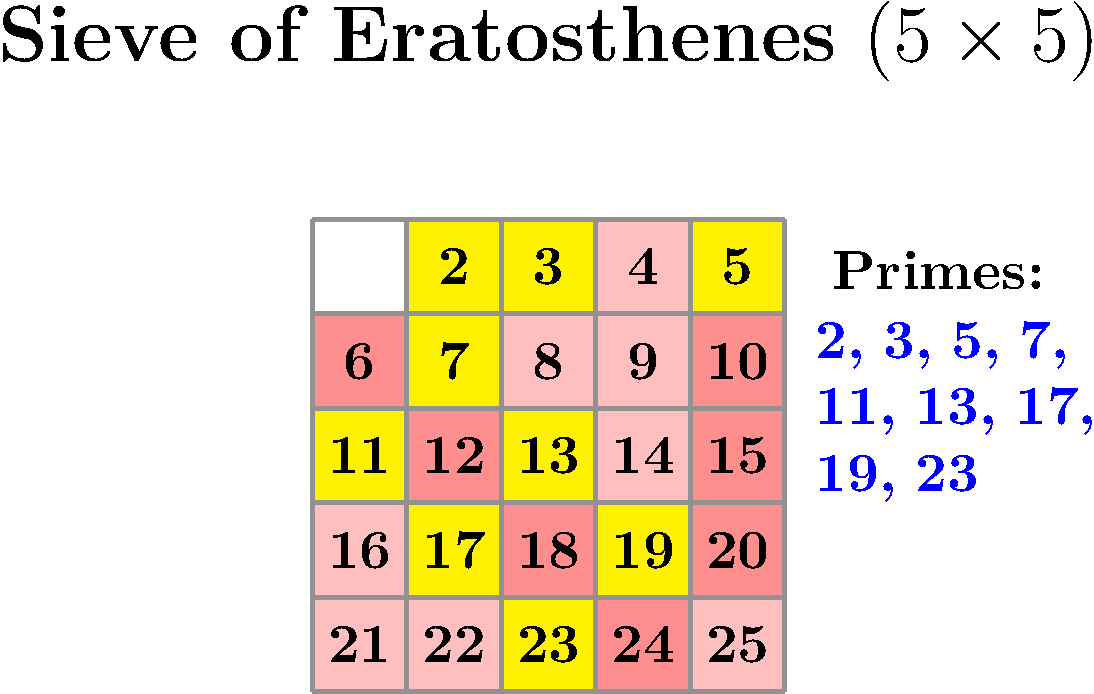
We can take this sieve as an example of sequential algorithms that need to be rethought if we want to take advantage of multiple threads of execution. This is important because during the last several years the computing power of a single thread has stagnated. However, CPUs are still growing in computing power by getting more and more cores over time¹.

At the current pace of change in the hardware space, the bottleneck for harnessing this computing power is going to be the scarcity of developers with knowledge on concurrency and parallelism and the use of inadequate tools and languages.

One of the paradigms that can be handy for this purpose is the actor model. It can be summarized as an extension to object orientation² in which objects run concurrently and the messages (method invocations) among them are asynchronous: every actor has a mailbox and process its messages one-by-one. In other words, this model has the property of having explicit parallelism built into it. Hewitt explains it way better than me.

Lets look at the Eratosthenes sieve through the actor model lenses looking for parallelization. We should replace the big table of numbers by a series of actors sending messages and doing work in parallel. One way to do it is to create a chain of actors that is fed with all the candidate numbers from 2 to N. The first number an actor receive become its prime number P and, from that point on, the following candidates are discarded when divisible by P and passed to the next actor otherwise.

Crappy visualization of the parallel Eratosthenes sieve concocted by me.

We can code this in very few lines using Scala and Akka (listing). We just need to create a class extending Actor whose initial behavior is specified by pattern matching in the receive method.

class Filter extends Actor {

  private var prime: Int = _

  override def receive: Receive = {

    case NoMoreCandidates =>
      println("No more candidates")
      println(s"Spent just ${System.currentTimeMillis() - start} millis")
      System.exit(0)

    case firstCandidate: Int =>
      prime = firstCandidate
      println(s"$prime found")
      context.become(filtering(context.actorOf(Props[Filter])))
  }

  private def filtering(successor: ActorRef): Receive = {
    case candidate: Int if candidate % prime == 0 => // Drop candidate
    case other => successor ! other
  }
}

This actor is waiting for a number (firstCandidate) to keep it as a newly found prime and then switches to the filtering behavior in which it drops any multiple of prime and pass along anything else. The chain of actors grows every time a new prime is found so the potential for parallelism grows over time.

Another notable thing is the sentinel value NoMoreCandidates, just a simple case object, used to coordinate an orderly execution stop.

case object NoMoreCandidates

The rest of the program is just creating the first actor and feeding it with the candidate numbers.

val MaxNumber = 500000
val start = System.currentTimeMillis()
val system = ActorSystem("sieve")
val sieve = system.actorOf(Props[Filter])
(2 to MaxNumber).foreach(sieve ! _)
sieve ! NoMoreCandidates
system.awaitTermination()

This implementation is short, clear and has the nice property of using the 100% of my four cores for about 110 seconds but has some problems. One of them is related with the initialization code sending 500001 messages as fast as it can produce them. This can produce awkward spikes in memory consumption and problems with the receiver actor inbox. Another related problem is the overhead of sending so much messages compared with just comparing the remainders of the candidates and the already found primes.

We can solve the first problem and mitigate the second by introducing backpressure and grouping the candidate numbers in chunks. Backpressure is, no more, no less, letting the intermediate elements of a distributed system to provide rate-adjusting feedback. There are many ways to do it like the TCP send window but for this example we will use the following rules:

• Filter actors won’t send candidates until explicitly asked for it by its successor in the chain by the new message GetCandidates.
• Filter actors will keep asking for candidates and filtering the results until having at least MinChunkSize candidates.
• We will have an additional candidate generator actor able to understand the GetCandidates message and sending the candidates in chunks of size DefaultChunkSize.

Implementing takes three times as many lines of code and introduces many subtle details to sort out but the execution time plummets one order of magnitude to just 18 seconds. I am not discussing the resulting code line by line to keep this post short but you can take a look at the complete listing.

What about the communication overhead problem? For the same first 500k numbers it takes 900ms so this parallelization strategy is not very good for this problem. Communication time dominates because I have just 4 cores and the basic steps are very simple.

But don’t despair as lessons learned are greatly valuable: we should expect confronting more computing-intensive problems with thousands of cores at our disposal in the following years.